
| Go Articles
|
 | |
| Setpiece Kos |
The way the ko in the Kato-Kobayashi game from the previous article was unsettled for so long indicates the slow and limited profitability of some kos. I think dan players, anyway, will take the point. It hung around because it wasn't urgent in the way other parts of the board more truly were. Players coming up to dan level do start to get a feel for the real usefulness of sente, and often over-correct, omitting plays they shouldn't. That is something to get over, by balancing up notions of the positive value of influential positions (typically completed in gote) and the negative value of weak groups arising from neglect of plays for security. What will be said in this article is abstract, but it rather assumes this sort of practical grasp as background.
The reason for thinking that the theory given here already isn't enough can be explained. So far the way to take into account the 'climate' in which a ko may be fought has in numerical terms comes down to intelligent application of miai counting. If there are alternate ways to play out a local position, which involve different tally changes, one does a price comparison on the basis of the value of a single play in the environment.
The trouble with this approach is that it is shopping, rather than playing a game. You may think that you are in charge of the game, and can direct play down a favourable avenue according to calculations. But your opponent may, just as likely, have alternate ways to play, and will vary strategy between them according to circumstances - in particular according to the current value of sente.
Therefore the phenomenon of break points demarcating strategy A from strategy B in playing out a position cannot in general be approached in a purely self-centred way. I may calculate that strategy A is superior until the temperature t in the game drops below a certain value. But my opponent too is entitled to switch strategies, and may do so quite rationally at a different temperature.
This area of theory is what is meant by thermography in Combinatorial Game Theory. I am no great believer in mathematics in go for its own sake, despite - perhaps because of - having a background in mathematics myself. It doesn't have much to do with professional players' normal approach, as far as I can tell; and the kind of mathematics that denatures one's intuition for the game can safely be taken as no good. It is essentially impossible, though, to connect up what I have written so far here to current ko research, without tackling this area.
The step forward to take is to consider strategy over the whole temperature range, up from 0 to high-energy (anything over 20 in normal go). Temperature 0 means 'penultimate plays': we can assume the game ends when the local situation we are examining is played out. Many games do end, for example, with a minimal ko (Japanese hanko, the so-called 'half-point ko'): and some are decided by its result.
What about the other end of the scale? General theory as well as normal practice in counting the board position indicate what to do: one counts territory on the assumption that each side gets in its sente endgame plays. No more and no less: no one can afford to take gote if sente is large enough. This is the exact opposite of the situation at temperature 0, where sente is of no use to anyone.
It is in this setting that we wrestle with putting plays in delimited regions of the board into context. Strategy cannot be described in a way that is uniform over temperature: there will be points of transition from one way of playing to another. The new concept to be introduced is first to plot a graph rather than concentrate on calculation of the value of t where a particular change takes place.
The fundamental example is a gote/sente change. Imagine an endgame position in which a choice of ways to play offers itself: I can take sente, or accept gote for a larger gain in points. Here is a very common example:
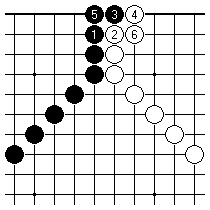
We are looking only at the top edge here. Black can play this way and take sente, at an early stage of the endgame, because Black's cut at 6 is very big if White fails to connect there. On the other hand Black 1 here is a large gote play, allowing the follow-up with Black 5 that ends in sente, for a total swing of 14 points compared to White playing the same way against Black.
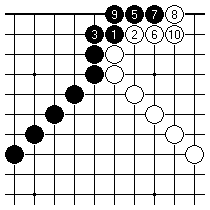
Evidently Black's second way of playing gives up sente for four extra points. We can express that by saying that the sente play is worth ten points. If we use miai counting, the first way of playing is 10 points and the second way 7 points. In a sense therefore one will expect that retaining sente is preferred here, under normal circumstances. But it seems worth pointing out that miai counting is, on the face of it, a tool for comparing the value of plays in different parts of the board. What are we doing, exactly, when we apply it to the comparison of different options in playing out the same position?
Let's draw what we'll call the profile of this position.
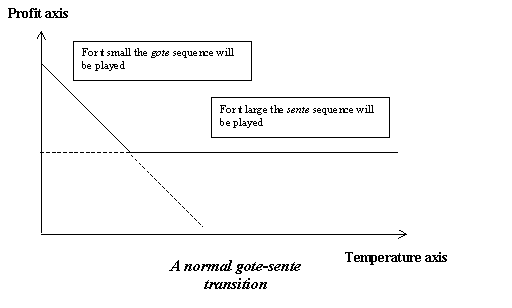
It will look like the graphic. The horizontal line extending to the right should be at height 10, and the sloping line at the left end should have gradient -1, crossing the axis at 14. What miai counting tells us is to take into account the extra one black stone in the first diagram compared to the second. In this graphical method we draw the lines y = 14 - x and y = 10, which therefore intersect at x = 4. This expresses what we could have said before: sente can be given up for four extra points, only if the value of sente, which is a name for temperature, is at most 4.
So far this is only a way of presenting the same data as a picture. It does make it easier to explain some points:
The general relation to tally reckoning and miai counting is clear enough: comparing a gain of a points with m extra stones, with b points by using n extra stones, we must look somehow at (a - b)/(m - n), the profit per additional stone assuming m and n are different. We can do this by equating a - mt with b - nt, and solving. The graphical method does this, while fixing a degree of freedom within the model. The gradient of the line for a gote play is set to be -1: that is, we regard a gote play as costing one extra stone. That is the reasonable convention to take here, because then the lines for sente plays come out horizontal. But it does again indicate that this is a shift from the usage for miai counting for comparisons in different areas: we treating the figure of 7 points miai for the gote play in the example as a quite different style of accounting for what is going on, highly relevant to why play in that position, but not a number that relates directly to how to play. It tells us about the vertical positioning of two lines that move up and down by the same amount according to a reference diagram like the second one above, but played out for White rather than Black.
This may seem a long and perhaps too apologetic discussion of a simple profile graph. The fact is that profiles may in interesting cases become rather complex, and then the interpretation becomes much tougher unless the basic type of example is something felt to be quite natural.
The decision-making process based on profiles takes the temperature t as a variable about which the players are fully informed (of course this is already an assumption about powerful reading and counting); and therefore available for use in a given position. The way profiles are combined isn't mysterious - it's the ordinary minimax idea but with the variable t carried along. That is, considering the upper region of the profile graph as defining it, these regions intersect when there are different options to combine. Because 'up' in a zero-sum game is assigned to the player given positive scores (conventionally Black), we have to understand that White is allowed to read 'upper' with the opposite sense.
The temperature itself controlled by the course of the game: in the conventional way of playing the opening and endgame it is fairly reasonable to think of it as tied closely to the occupation of 'big points', but in the middlegame phase that is much harder to accept. One expects temperature to decrease, with some excursions caused by threat plays which are effectively forcing, or fights that break out and have to be resolved before the game can proceed further in other areas. That actually doesn't say very much - the trend of temperature is to decrease, but in a running fight it may be increasing for a while as players add stones to unsettled groups they can't afford to sacrifice, and then when the groups become safe the temperature will drop back. The proper explanation of triple ko and other similar repetitive positions is that a long-cycle repetition occurs (which it can as soon as there are three kos on the board) which prevents the temperature dropping, a much rarer phenomenon than the mere possibility of simple looping.
This article has been intended as a gentle introduction to thermography (for my own benefit as much as anyone else's). The definitive presentation is in terms of a thermograph, which is made by taking Black's and White's profiles of a position, re-orienting them so that the ultimate horizontal lines become vertical and gluing them along that line (then called the mast). The effect is, for example, to take a line of gradient -2 for Black's play, as we would draw for a profile, and to make it have gradient 1/2 - slow uphill work. This brings the language used in this article to the point of compatibility with that of the games theory classic Winning Ways by Berlekamp, Conway and Guy.
I (unlike a number of enthusiasts for theory in go) don't recommend anyone to start off reading the literature on Combinatorial Game Theory (CGT), as the theory is now called, in the search of insight into go. I was an academic colleague of John Conway's for a number of years, and a go player, and never then made the leap of connecting go with CGT, though others in my club and department such as the late Frank Adams did. I come to this quite late, in order to catch up with the research being carried on by Elwyn Berlekamp and his school. Combinatorics isn't a soft option, whatever anyone may tell you otherwise. The piece of history attributing to watching go being played some of the inspiration behind Conway's input into CGT seems well-attested. It would be nice to think that CGT could return the compliment to go; but what combinatorics models most effectively is often related to its precursor across a serious transition (for example, formal languages and natural languages).
The collaborators on the
Sensei's Library site,
notably Bill Spight, have been wrestling with the
expository problem posed by the gulf between go and CGT
ways of thinking. This is still work in progress, but
see the CGT path
there if you'd like to approach this area and are wisely
reluctant to read hundred of pages of theory first.
| Posted 4 November 2002. Copyright © 2002 Charles Matthews | ||
| Previous edition | Index | Next edition |